

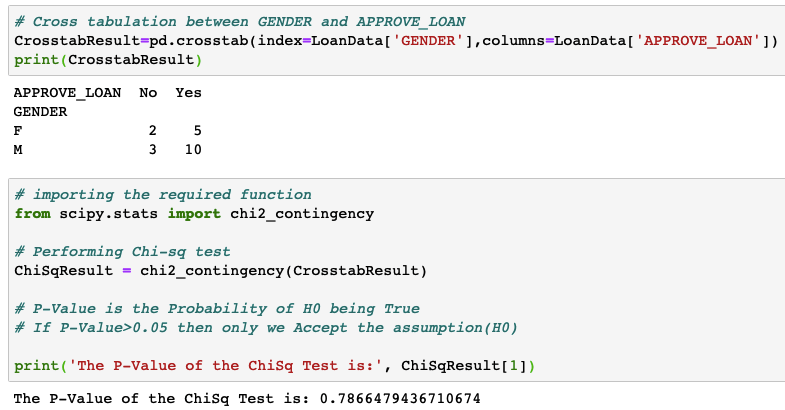
With above example it would spit a decrease of this probable coef-err fromĪnd the absolute size of this error measure seems to be too low for just 4 points of data! But thus it is not sensitive to above considerations about 'boring' data. Probable error of r = 0.6745*(1-r**2)/sqrt(N)Ī simple function of r and N - quite what I expected above roughly for the N-only dep. In MATLAB, corr(X) calculates Pearsons correlation coefficient along with p-value.ĭoes anybody know how this prob.-value is computed/motivated? Such thing would be very helpful for numpy/scipy too. I remember once I saw somewhere a formula for an error range of the corrcoef. But this 'boring data' should not make the error to go down simply ~1/sqrt(N). I'd expect: the little increase of r is ok. Got it - or not? Thus lower coefs require naturally a coef-err to be useful in practice. More interesting realworld cases: For example I see a lower correlation on lots of points - maybe coef=0.05. Yet it depends more complexly on the mean value of the coef and on the distribution at all. One would expect the error range to drop simply with # of points. With big coef's and lots of distributed data the coef is very good by itself - its error range err(N) only approx ~ 1/sqrt(N)
You get a perfect 1.0 with 2 ( or 3 - see below ) points. I'd need a quality measure (coef**2) and to know how much I can rely on it (coef-err). )īasically the first need is to analyse lots of x,y data and check for linear dependencies. ( before you proceed to a model or to class-learning. coef first before going on to any models, seems to be a more stable approach for the first step in data mining. Think the difference is little in practice - when you head for usable diagonals. >Is there a ready made function in numpy/scipy to compute the correlation y=mx+o of an X and Y fast: That is made terrible by our own mad attempt to interpret it as though it had "I have come to believe that the whole world is an enigma, a harmless enigma The second does both the x and y marginalĭistributions need to be normal. The difference between the two models is that the first places no restrictions Your correlation coefficient will be the off-diagonal term afterĭividing out the marginal standard deviations. You should instead estimate the mean vector and covariance matrix of Normal distribution" then "y=m*x+o" is not a particularly good representation of On the other hand, if your model is that "(x, y) is distributed as a bivariate Will be found in the estimates of m and o and the covariance matrix of the
"y=m*x+o" is correct, and all of the information that you can get from the data If your model is truly "y is a linear response given x with normal noise" then Is there a ready made function in numpy/scipy to compute the correlation y=mx+o of an X and Y fast:Īnd of course, those three parameters are not particularly meaningful together.


 0 kommentar(er)
0 kommentar(er)
